Por Pedro Ramos
Nova Iorque, outubro 2020
«Juro composto é a oitava maravilha do Mundo. Quem o entende, ganha-o. Quem o desconhece paga-o» – atribuído a Albert Einstein
Queridas filhas,
Proponho um jogo divertido. Peguem numa folha de papel. Dobrem-na a meio. Deve ser difícil de sentir, mas a espessura do papel duplicou. Dobrem de novo a meio. A espessura do papel dobrou de novo. Agora, a espessura do papel é quatro vezes a do papel original. Se duvidam contem as folhas dobradas uma em cima da outra. Talvez já comecem a sentir o papel mais espesso…. Dobrem de novo a terceira vez. Dobrem de novo. Continuem a dobrar. Não desistam!
Dobraram 17 vezes? O papel tem a vossa altura. Dobraram 25 vezes? O papel agora tem a altura do Empire State Building. Dobraram 40 vezes? O papel chega agora ao satélite que nos dá o GPS. Dobraram 42 vezes? O papel agora chega a Lua!
O que está a acontecer? Como é que uma coisa tão simples como uma dobra tem resultados tão espetaculares ao fim de algumas dezenas? Este é o poder dos juros compostos. Cada vez que dobramos o papel, dobramos não só o papel original, mas também todas as dobras do papel feitas antes.
O mesmo acontece em finanças. O juro de períodos anteriores transforma-se em capital para os períodos futuros. Vamos ilustrar com o exemplo de um depósito de 100 euros a uma taxa de juro de 10%. A tabela seguinte mostra a evolução do total do depósito (segunda coluna) e juros vencidos (terceira coluna) ao longo dos anos.
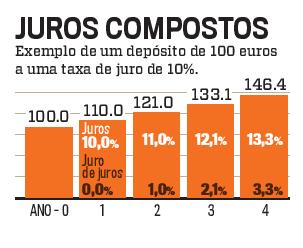Como podem ver o depósito continua a crescer a ritmos cada vez mais rápidos. Os juros de juros (calculados na última coluna) são os responsáveis por este efeito bola de neve. Por exemplo, no segundo ano os juros são 11 euros e não os 10 euros cobrados no ano 1 (100×10%=10 euros). Porquê? Porque o depósito no ano 2 é de 110 euros, dado que os 10 euros de juros vencidos no ano 1 não foram levantados. Assim temos 11 euros = 10%x110 euros. A diferença entre os 11 euros de juros do ano 2 e os 10 euros de juros do ano 1 são os Juros de Juros. Pode parecer uma diferença pequena, mas tem um impacto enorme. Especialmente em prazos longos. A tabela seguinte ilustra quanto será o depósito a diferentes prazos e com diferentes taxas de juro:
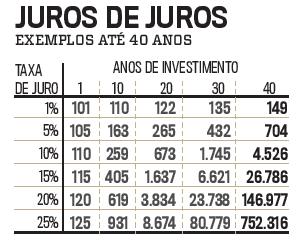
Esta tabela ensina duas importantes lições.
Primeira: quanto maior o tempo de investimento maiores os juros de juros. Por exemplo, o depósito de 100 euros a uma taxa de 15% rende 1,673 euros ao fim de 20 anos e 26,786 euros ao fim de 40 anos! Assim temos juros de 1,573 euros nos primeiros 20 anos e de 25,750 euros (26,786 – 1,637) nos segundos 20 anos. Quando devem começar a investir? Ontem! Quanto mais cedo melhor! E mantenham-se de boa saúde para durarem muitos anos.
Segunda: quanto maior a taxa de investimento, melhores os resultados. Ao fim de 40 anos o depósito a uma taxa de 15% rende 26,786 euros. Mas se a taxa for de 25%, o depósito rende 752,316 euros. Que diferença 10 pontos percentuais fazem!
Nas próximas cartas vamos falar de estratégias para melhorar as taxas obtidas nas nossas aplicações financeiras. Ah, e o exemplo de dobrar a folha de papel? A taxa de juro nesse caso é 100%…
